決定木をフルスクラッチで書けるようになろう (CART)

この記事は慶應理工アドベントカレンダー2021の18日目の記事です.

昨日の記事はこちら.

ainnooo.hatenablog.com

アドカレに誘ってくださった @ainnoooさんがほんわかタイトルの記事書いてます. ちゃんとソケットあたりのコード読んでてすごい.

はじめに
本記事の目的
決定木とは
問いを整理する
不純度: 「如何に分割するか？」
木を成長させてみよう
木の剪定
動かしてみよう
iris以外のデータでも試してみよう.
おわりに

はじめに

改めまして. 研究室配属が決まって一安心しているJ科B3のYuWdです.

久しぶりに何か書いてみようということでアドカレに登録したものの, 怠惰ゆえに当日18日目(2:00AM)から書き始めております. アホです.

あまり時間がないので, 個人的にタイムリーなことを書きたい.... ということで, 研究室の面接で提出したコードをそのまま流用する形で, 「決定木」についての記事を書いていきたいと思います.

本記事の目的

本記事では二分木ベースのCARTについて説明します. ID3やC4.5など, 多分木ベースの決定木は扱いません.

対象となる読者は, 決定木のことをよく知らない人や, 一度もフルスクラッチで実装したことない人を想定しています.

読者の目標は, 決定木(CART)の概要を理解し, 実際にnumpyだけで実装できるようになることです. この記事を理解すれば, 以下のような結果を生成する決定木をソラで書けるようになることでしょう.

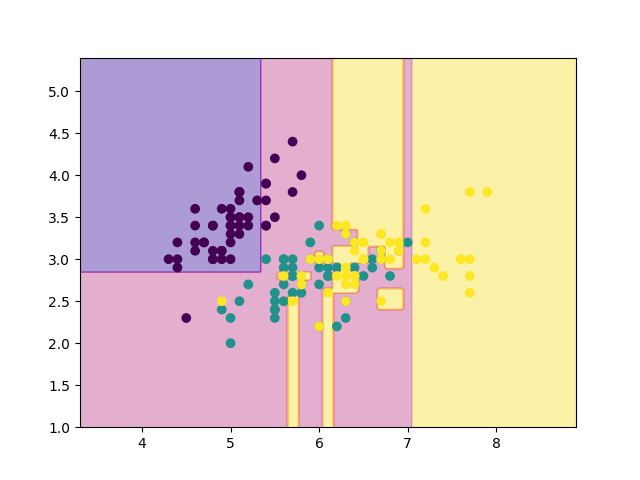
本記事では, 以下の項目を扱います.

空間の分割
木の剪定とCV
グリッドサーチによるハイパーパラメータの調整(ただの全探索)

本記事を読むのに必要な知識を以下に箇条書きで示しておきます.

高校程度の数学力
numpyの扱い方
木に対する基礎的な理解
DFS

注: 今回, pandasは扱いません. pandasは使い方を誤るとかなり重たくなってしまうので要注意です.

決定木とは

決定木といえば, 下のようなイメージが頭の中に立ち上がるかもしれません.

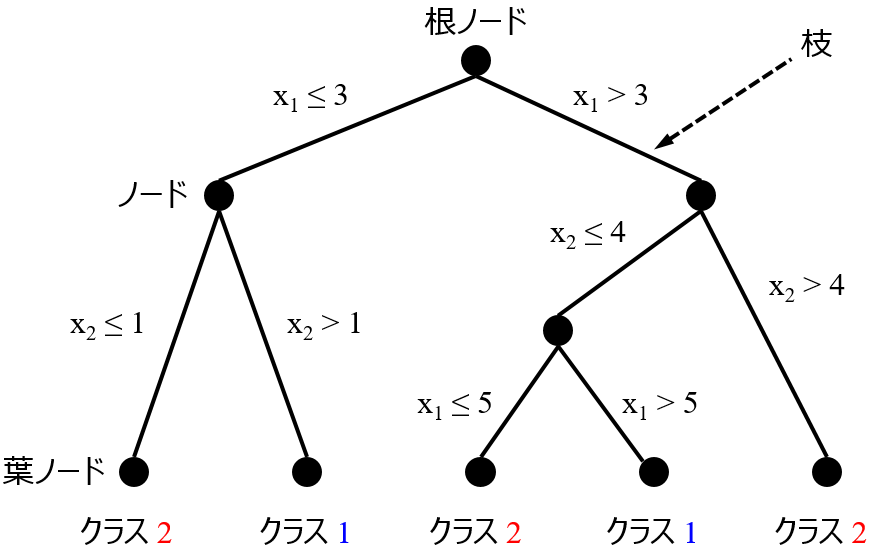
f:id:yuwd:20211218021412p:plain:h300 — 決定木ってこんなヤツ？ *1

こうした「木の形」が頭にあると, どうしても決定木という手法が摩訶不思議なものであるかのように見えてきます. ですが, 実際のカラクリは至極単純なものです. 簡単のため, まずは2つの特徴量 $x_1, x_2$ を扱うモデルを考えてみましょう.

下に示すのは, sklearn.datasetsのirisのデータセットを2次元上にプロットしたものです. 横軸を $x_1$ , 縦軸を $x_2$ とします.

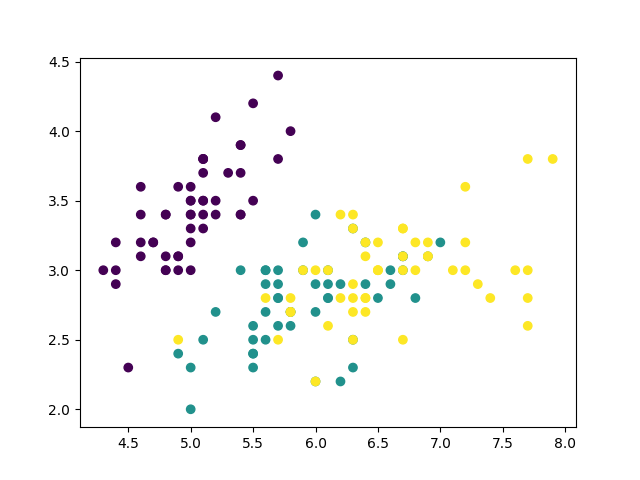
f:id:yuwd:20211218022545p:plain — irisのデータセット

上の画像を眺めながら, このデータセットに対する識別器として, 有効かつ最も単純なモデルはどのようなものか考えてみてください.

NN系の手法やSVM(+カーネル法)が頭をよぎる人もいるかもしれません. しかし, これらの手法は一般に, 非線形関数を用いてゴニョゴニョする輩たちです.

回帰やパーセプトロンのような手法が想起される方がいらっしゃるかもしれませんね. しかし, これら以上に単純な発想の方法があるのです.

有効かつ最も単純な手法とは何か. それは, 各データ点をいい感じに分割できるように長方形をいっぱい作ることです.

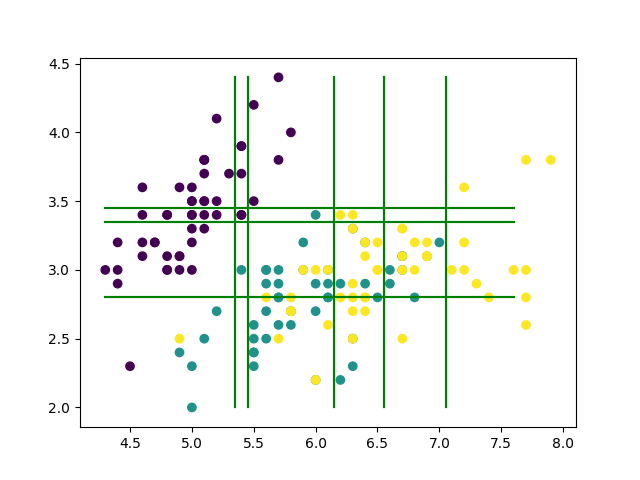
つまり, 2次元平面であれば上の画像のように, 特徴量 $x_1, x_2$ ごとに直線を引いていき, 領域をいい感じに分割していけば良いのです.

この考え方を $d$ 次元(特徴量 $d$ 個の場合)に拡張しましょう. すなわち, 決定木とは「 $d$ 次元空間上に $d-1$ 次元の超平面を多数生成し, 分割領域を分けて識別器を表現(記述)する」手法なのです.

では実際, どのように空間を分割すれば良いのでしょうか.

軸(=特徴量)の選択に関しては, 適当な順番で巡回させれば良いですから, 今回は $x_1, x_2, ... ,x_N, x_1, ...$ と選択することとして, まずは以下のように分割すれば良いことがわかります.

軸 $x$ を選択 ( $x_1, x_2, ... ,x_N, x_1, ...$ )
各データを $x$ に対してソート.
隣接点同士の中点を計算し, その中点を分割点の候補とする.
何らかの評価基準で分割点を評価する.

問題は, 4番目の「何らかの評価基準で分割点を評価する」方法です.

問いを整理する

問題に取り組む前に, まずは問いと設定を整理しましょう.

今回は, 特徴量 $N$ 個で, クラスが $K$ 個 ( $C_1, C_2, ... , C_k$ )のデータが与えられたとき, それらのクラスを識別する決定木を考えます. ノードの分割は, 領域の分割と同等の関係にありますから, 木の深さごとに, 分割対象の軸が( $x_1, x_2, ... ,x_N, x_1, ...$ )と巡回していきます. またノードを分割する規則として, 必ず左ノードは小なりイコール, 右ノードは大なりを意味することにします.

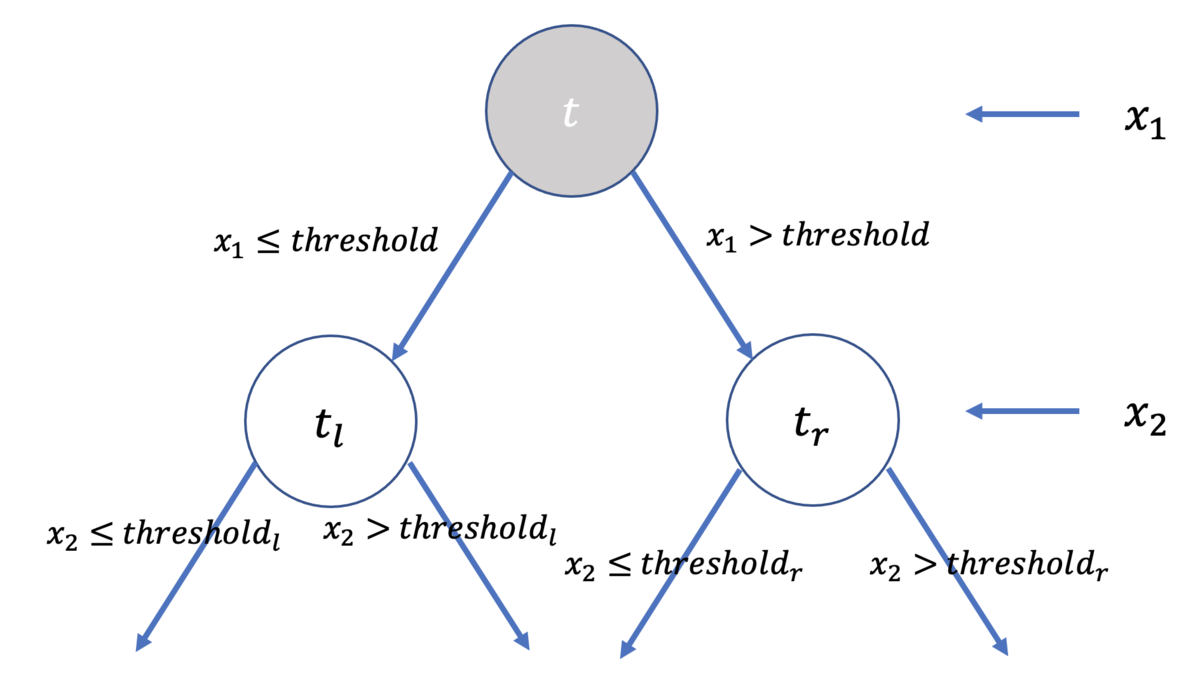
f:id:yuwd:20211218182306p:plain — ノード $t$ を分割

私達が直面している問題は, 上図における $threshold$ を如何に定めるべきなのか, ということなわけです.

不純度: 「如何に分割するか？」

ノード $t$ をノード $t_l$ , $t_r$ とに分割する場合を考えてみましょう. 以下に示すのは, ノード $t$ を分割する様子です. 左側で示した決定木は, 右側のように分割されていることと対応します.

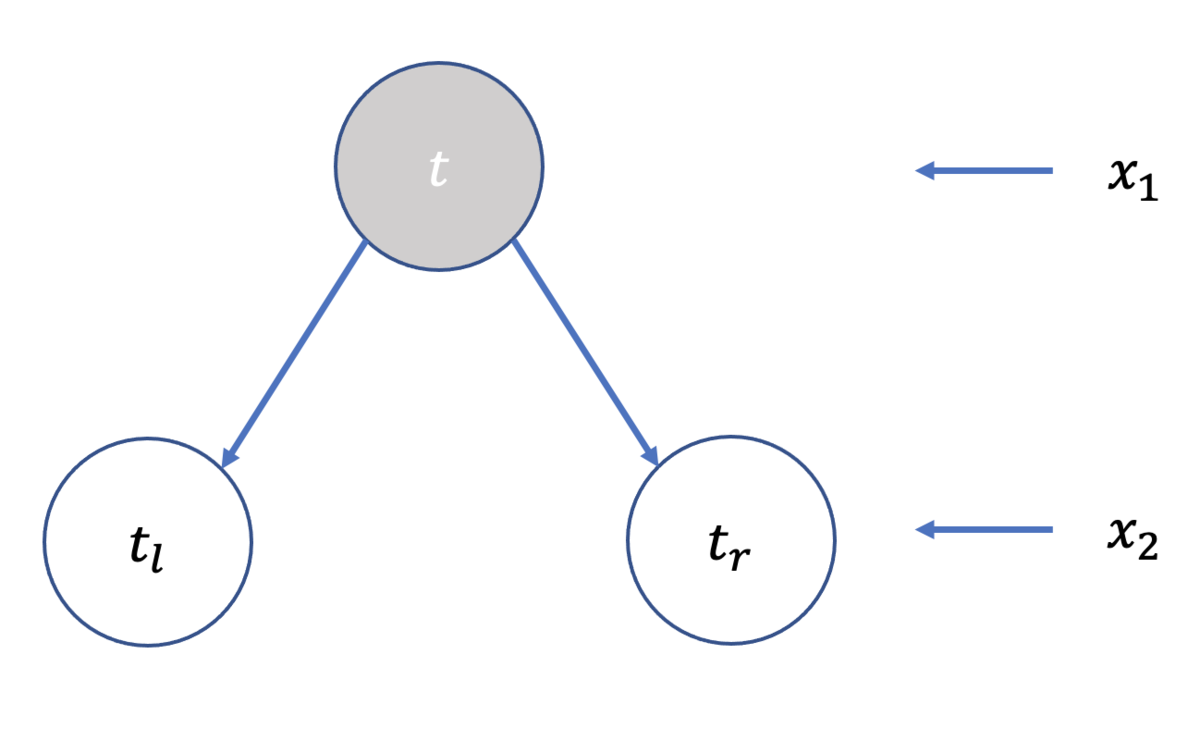
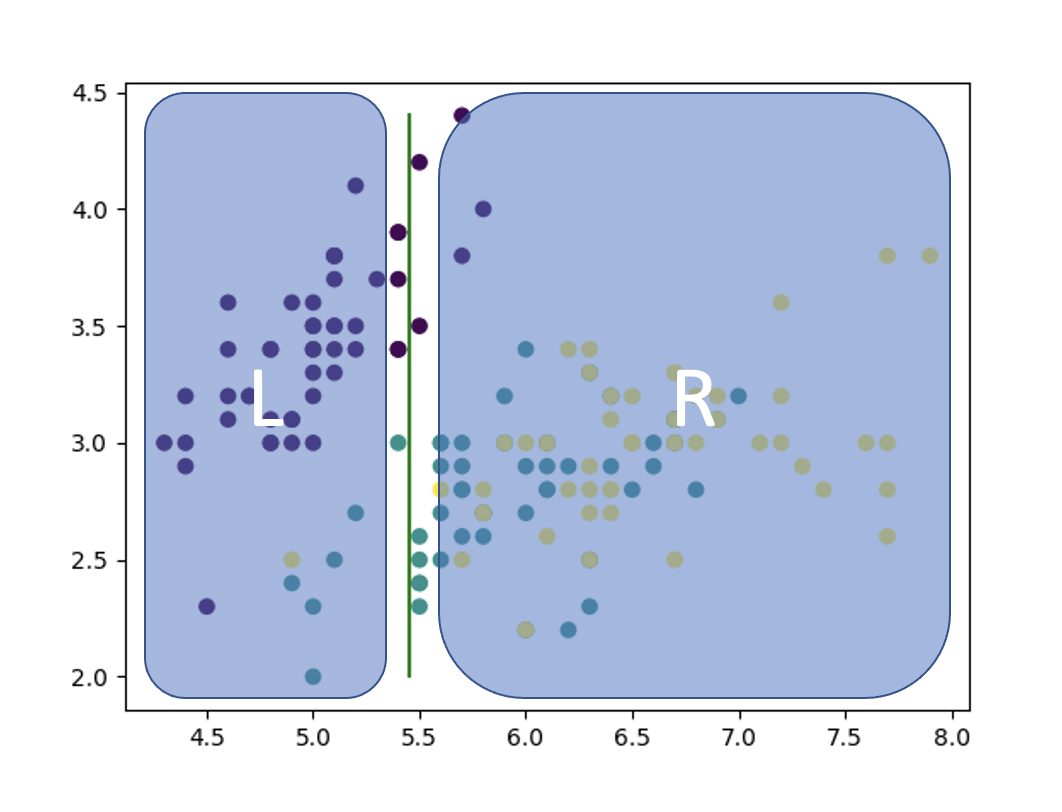
f:id:yuwd:20211218034544p:plain:w300 — ノード $t$ をノード $t_r$ , $t_r$ に分割

f:id:yuwd:20211218034541p:plain:w300 — ノード $t$ をノード $t_r$ , $t_r$ に分割

分割点を評価するにはどうすれば良いでしょうか. こういうときは極端な例を考えてみると感覚がつかめることが多々あります. まず, 完全に分割された状態を考えてみると, ある分割領域 $S$ に着目したとき, $S$ 内にあるデータ点のクラスが一つだけの状態が最も好ましい状況です. では逆に, 最も好ましくないのはどのような状態か. それは, $S$ 内にあるデータ点のクラスが最もバラバラな場合, すなわち, $S$ 内部にクラス $C_1, ... , C_K$ 全てのデータが均等に入っている状態です.

CARTでは分割点を評価する基準として「不純度」(Impurity)と呼ばれる指標を扱います. 不純度 $I(t)$ が

$\displaystyle I(t) = \phi(P(C_i \mid t), ... , P(C_K \mid t))$

と表されるとき,

$\phi(z_1,z_2,...z_k)$ は, 上での議論の通り, 以下のような条件を満たせば良いことがわかります.

$\forall i, z_i = \frac{1}{K}$ ならば, $\phi(z_1,z_2,...z_k)$ が $max$ .
$\exists j, \forall i \neq j, z_j = 1, z_i = 0$ ならば, $\phi(z_1,z_2,...z_k)$ が $min$ .
$\phi(z_1,z_2,...z_k)$ は $z_1,z_2,...z_k$ の順序に依存しない.

代表的な不純度には以下の３つがありますが, CARTでは主にジニ係数を使います.

ノード $t$ における誤り率

$\displaystyle I(t) = 1 - \max_i P(C_i \mid t)$

ノード $t$ における交差エントロピー(cross-entropy)

$\displaystyle I(t) = - \sum_{i=1}^K P(C_i \mid t) \ln P(C_i \mid t)$

ノード $t$ におけるジニ係数 (gini-index)

$\displaystyle I(t) = \sum_{i=1}^K \sum_{j \ne i} P(C_i \mid t) P(C_j \mid t) = 1 - \sum_{i=1}^K P^2 (C_i \mid t)$

それぞれの式の意味は, ぐっと睨めば理解できると思います.

ジニ係数の意味するとこがよくわからない人は, 次のように考えると良いでしょう. すなわち, ノード $t$ と対応する分割領域 $S_t$ において, クラス $C_i$ に着目したとき, $C_i$ 以外のクラスのデータがその分割領域にどれだけ入っているかを, 全ての $i$ について計算・総和することで, 分割領域 $S_t$ がいかにpureではないかを評価しています.

以上より, ノード $t$ を分割するには, 各分割点の候補についてそれぞれ不純度 $I(t)$ を計算し, 不純度 $I(t)$ が最も小さい候補点を採用してあげれば良いことがわかります.

具体的に, CARTでは以下のように行います.

$N$ 個のデータ点に関して, それぞれ隣接するデータ点との中点を候補点とする. (候補点は $N-1$ 個できる)
$\Delta I=I(t)-(p_l I(t_l)+p_r I(t_r))$ が最も大きくなる候補点を採用する.
その点を $threshold$ として領域を分割.

ただし, $p_l, p_r$ とは, それぞれ左ノード, 右ノードに含まれるデータ数の比率(濃度)を指します. すなわち,

$\displaystyle p_l = P(x \in L | x \in S_t) = \frac{p(t_l)}{p(t)}$

$\displaystyle p_r = P(x \in R | x \in S_t) = \frac{p(t_r)}{p(t)}$

として, 不純度に重みをつけてあげるのです.

木を成長させてみよう

これで大方決定木のことが理解できたはずなので, やっと実装できそうです.

まずは, ノードを表現するNodeを用意しましょう. X, Yはそれぞれ, 特徴量行列と目的変数のベクトルです.

import numpy as np
import matplotlib.pyplot as plt
import time
PLOT = 1

class Node:  # 決定木のノード
    def __init__(self, X, Y, depth=0):
        self.left = None
        self.right = None
        self.feature = None
        self.threshold = None

        self.X = X
        self.Y = Y
        self.features = [i for i in range(np.shape(X)[1])]

        self.depth = depth
        self.class_table = np.bincount(Y)
        self.class_label = np.argmax(self.class_table)  # arg{max{count(x)}}

次に, 決定木を表現するTreeを用意しましょう.

class Tree:  # 決定木
    def __init__(self, X, Y, max_depth): 
        self.root = Node(X, Y)
        self.X = X
        self.Y = Y
        self.max_depth = max_depth

        min_max_table = []
        for i in range(np.shape(X)[1]):
            min_max_table.append([min(X[:,i]), max(X[:,i])])
        self.min_max_table = min_max_table
        

    def gini(self, pair):  # ジニ係数を計算
        if sum(pair) == 0:
            return 0.0
        probabilities = pair / sum(pair)
        gini = 1 - sum(probabilities**2)
        return gini

    def get_mean_array(self, x):  # 各中点を計算
        if len(x) == 0:
            return []
        return np.convolve(x, np.ones(2), mode="valid") / 2

    def get_gini(self, X, Y, feature=None, value=None, separate_type=None):  # 分割後のジニ係数を計算
        if separate_type == None:
            count_table = np.bincount(Y)
        elif separate_type == "left":
            count_table = np.bincount(Y[X[:, feature] <= value])
        elif separate_type == "right":
            count_table = np.bincount(Y[X[:, feature] > value])

        count = sum(count_table)
        half_gini = self.gini(count_table)
        return count, half_gini

    def split(self, node):  # 適切な分割点を探索
        X, Y = node.X, node.Y
        _, gini = self.get_gini(X, Y)

        maximum = -1
        best = None
        threshold = None

        for feature in node.features:
            if len(np.unique(X[:, feature])) <= 1:
                continue
            ix = X[:, feature].argsort()
            mean_array = self.get_mean_array(np.unique(X[ix, feature]))
            for value in mean_array:  # 各中点で分割してジニ係数を計算
                lcount, lgini =\
                    self.get_gini(X[ix], Y[ix], feature, value, "left")
                rcount, rgini =\
                    self.get_gini(X[ix], Y[ix], feature, value, "right")

                count = lcount + rcount
                l_probability = lcount / count
                r_probability = rcount / count

                gain = gini - (l_probability * lgini + r_probability * rgini)
                assert gain >= 0
                if gain > maximum:  # chmax
                    best = feature
                    threshold = value
                    maximum = gain

        if best is None:
            assert len(np.unique(X[:, feature])) <= 1
        return (best, threshold)

    def fit(self):  # 決定木を生成
        self.grow(node=self.root)

    def grow(self, node):  # node以降で木を成長させる
        if node.depth >= self.max_depth:
            return

        X, Y = node.X, node.Y
        feature, threshold = self.split(node)

        if feature is None:
            return
        node.feature = feature
        node.threshold = threshold
        il, ir = X[:, feature] <= threshold, X[:, feature] > threshold
        ndepth = node.depth + 1
        node.left = Node(
            X[il],
            Y[il],
            depth=ndepth,
        )
        node.right = Node(
            X[ir],
            Y[ir],
            depth=ndepth,
        )

        self.grow(node.left)
        self.grow(node.right)

    def draw(self):  # 分割区間をグラフに表示
        if not PLOT:
            return
        stack = [self.root]
        terminals = []
        while len(stack):  # DFS
            current = stack.pop()
            if current.left is not None:
                stack.append(current.left)
            if current.right is not None:
                stack.append(current.right)

            if current.feature is None:
                continue

            if not current.feature:
                plt.plot([current.threshold, current.threshold],
                         self.min_max_table[~current.feature], color="green")
            else:
                plt.plot(self.min_max_table[~current.feature], [current.threshold,
                                  current.threshold], color="green")
    def predict(self, X):  # 識別器
        predictions = np.zeros_like(X[:,0])
        for i,x in enumerate(X):
            values = {}
            for feature in self.root.features:
                values.update({feature: x[feature]})

            current = self.root
            while current.depth < self.max_depth and current.feature is not None:
                next = current.left if values[current.feature] < current.threshold else current.right
                if next is not None:
                    current = next
                else:
                    break
            predictions[i] = current.class_label

        return predictions

最後に, irisのデータセットを丸々使って学習させてみましょう.

def main():
    from sklearn.datasets import load_iris

    # Data-set
    iris = load_iris()
    X, Y = iris.data[:, :2], iris.target

    # Train & Test
    tree = Tree(np.array(X), np.array(Y), max_depth=100)
    tree.fit()
    error = test(X, Y, tree)

    # Plot & Draw
    plt.scatter(X[:, 0], X[:, 1], c=Y)
    tree.draw()
    plt.savefig("result.png")
    print("error:", round(error, 3)) # 再代入誤り率

if __name__ == "__main__":
    start = time.time()
    main()
    elapsed_time = time.time() - start
    print("time:{:.2f}[sec]".format(elapsed_time))

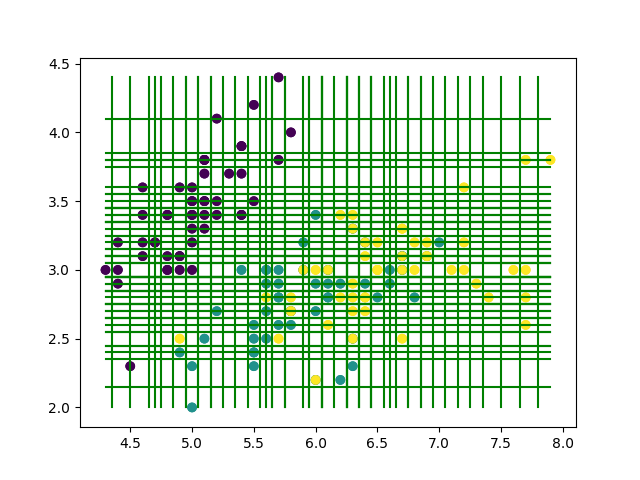
f:id:yuwd:20211218155336p:plain — 実行してみた

上の結果を見てみると, 確かにきちんと分割されていそうです！！

木の剪定

賢明なみなさんであれば, 先程の結果を見て, 汎化性能が極端に悪そうなことに気がつくと思います.

どうすれば汎化性能が向上するでしょうか. max_depthをイジれば簡単に済むのですが, 実は少しだけ面白い手法があるんです.

ということで,次は「木の剪定」について説明していきます.

木の剪定とは, その名の通り, 適切なエッジを切り取って枝刈りすることを意味します. 木が複雑すぎるならば, 何かしらの基準でエッジを評価し, それを切り取ってしまえば良いのです.

ここで, いくつか重要な記号と式を導入します.

非終端ノード $t$ を根ノードとする部分木を $T_t$ とする.
終端ノードの集合を $\widetilde{T}$ とする.
終端ノード $t$ の誤り率は

$\displaystyle R(t) = \frac{M(t)}{N}$

任意のノード $t$ の誤り率は

$\displaystyle R(t) := (tの再代入誤り率) \times (周辺確率) = r(t)p(t)$

木全体の誤り率は

$\displaystyle R(T) := \sum_{t \in \widetilde{T}} R(t)$

木を剪定する基準はどのようなものが考えられるでしょうか. まずは感覚的に考えてみましょう.

木を剪定するときは, なるだけ複雑で誤りが大きくなるような部分木を削除したくなりますから,

$\displaystyle \frac{R(t) - R(T_t)}{|\widetilde{T_t}|}$

が最小なノード $t$ について, その部分木を全て削除してしまえば良いことがわかりますね. ただし, 最低一つは終端ノードが存在することが前提ですので, 式を以下のように修正しましょう.

$\displaystyle \frac{R(t) - R(T_t)}{|\widetilde{T_t}|-1}$

これで, 上式は必ず最低一つの終端ノードを持つことを加味して評価することになります. ということで, これっぽい式を頑張って導出しましょう. (以下, はじパタを参考にします.*2 )

まずは終端ノードの数にペナルティを課すことを考えます. すなわち, 正則化パラメータ $\alpha$ を用いて, ノード $t$ における評価関数 $R'(t, \alpha)$ を $R'(t, \alpha) := R(t) + \alpha$ と, また, 木全体における評価関数 $R'(T, \alpha)$ を $R'(T, \alpha) := R(T) + \alpha|\widetilde{T}|$ と定義します.

ここで, 正則化パラメータ $\alpha$ を大きくしていくことを考えてみると, 次第に $R'(T_t, \alpha)$ と $R'(t, \alpha)$ は互いに近づいていき, やがて同じ値となることがわかります.

このとき, 正則化パラメータ $\alpha$ は

$\displaystyle \alpha = \frac{R(t) - R(T_t)}{|\widetilde{T_t}|-1}$

となり, あら不思議. 今さっきの式と同じものが得られました.

はじパタではこの $g(t)$ を

$\displaystyle g(t) = \frac{R(t) - R(T_t)}{|\widetilde{T_t}|-1}$

ノード $t$ におけるリンクの強さと呼んでいます.

以上より, 次のようなアルゴリズムで木を剪定していけば良いこととなります. すなわち,

$\displaystyle \min_{t \in T\backslash\widetilde{T}}{g(t)} = \min_{t \in T\backslash\widetilde{T}}{\frac{R(t) - R(T_t)}{|\widetilde{T_t}|-1}}$

を満たすノード $t$ を探索し, 該当ノード $t$ より下のものは全て削除します.

(はてなブログってargmin使えないの？？？？)

剪定アルゴリズムが定まりました. では, 実装してみましょう.

ノードの探索ですが今回はDFSでやってみます.

## Node内

    def get_error(self):  # 1 - max{P(C_i|node=self)}
        table = self.class_table
        return sum(table) > 0 if 1 - max(table) / sum(table) else 1

## Tree内

    def prune(self):  # 木の剪定 (arg{min{g(x)}}の子孫を全て削除する)
        stack = [self.root]
        N = len(self.X)
        INF = 1 << 30
        mg = (INF, None)  # min_g, arg{min_g}
        while len(stack):  # DFS
            current = stack.pop()
            has_left = current.left is not None
            has_right = current.right is not None
            is_terminal = not has_left and not has_right

            if not is_terminal:  # 非終端ノードはg(node)を計算
                expr = self.g(current)
                if expr < mg[0] and current != self.root:
                    mg = (expr, current)

            if has_left:
                stack.append(current.left)
            if has_right:
                stack.append(current.right)

        alpha, target = mg
        if target is not None:
            target.left = None
            target.right = None

        return alpha

    def get_terminal_error(self, node):  # 終端nodeの誤り率 = M(t) / N , M(t):=総誤り数
        N = len(self.X)
        failure = 0
        for y in node.Y:
            failure += y != node.class_label

        return failure / N

    def get_nonterminal_error(self, node):  # 非終端nodeの誤り率 = 再代入誤り率 * 周辺確率
        p_t = len(node.X) / len(self.X)  # 周辺確率
        R_t = node.get_error() * p_t
        return R_t

    def g(self, node):  # g(t) = node_tのリンクの強さ
        R_t = self.get_nonterminal_error(node)
        stack = [node]
        terminals = 0
        R_T = 0
        while len(stack):  # DFS
            current = stack.pop()
            has_left = current.left is not None
            has_right = current.right is not None
            if has_left:
                stack.append(current.left)
            if has_right:
                stack.append(current.right)
            if not has_left and not has_right:
                R_T += self.get_terminal_error(current)
                terminals += 1

        alpha = R_t - R_T
        alpha /= (terminals - 1)
        return alpha

動かしてみよう

最終的なNodeとTreeは以下のようになります.

class Node:  # 決定木のノード
    def __init__(self, X, Y, depth=0):
        self.left = None
        self.right = None
        self.feature = None
        self.threshold = None

        self.X = X
        self.Y = Y
        self.features = [i for i in range(np.shape(X)[1])]

        self.depth = depth
        self.class_table = np.bincount(Y)
        self.class_label = np.argmax(self.class_table)  # arg{max{count(x)}}

    def get_error(self):  # 1 - max{P(C_i|node=self)}
        table = self.class_table
        return sum(table) > 0 if 1 - max(table) / sum(table) else 1

class Tree:  # 決定木
    def __init__(self, X, Y, max_depth): 
        self.root = Node(X, Y)
        self.X = X
        self.Y = Y
        self.max_depth = max_depth

        min_max_table = []
        for i in range(np.shape(X)[1]):
            min_max_table.append([min(X[:,i]), max(X[:,i])])
        self.min_max_table = min_max_table
        

    def gini(self, pair):  # ジニ係数を計算
        if sum(pair) == 0:
            return 0.0
        probabilities = pair / sum(pair)
        gini = 1 - sum(probabilities**2)
        return gini

    def get_mean_array(self, x):  # 各中点を計算
        if len(x) == 0:
            return []
        return np.convolve(x, np.ones(2), mode="valid") / 2

    def get_gini(self, X, Y, feature=None, value=None, separate_type=None):  # 分割後のジニ係数を計算
        if separate_type == None:
            count_table = np.bincount(Y)
        elif separate_type == "left":
            count_table = np.bincount(Y[X[:, feature] <= value])
        elif separate_type == "right":
            count_table = np.bincount(Y[X[:, feature] > value])

        count = sum(count_table)
        half_gini = self.gini(count_table)
        return count, half_gini

    def split(self, node):  # 適切な分割点を探索
        X, Y = node.X, node.Y
        _, gini = self.get_gini(X, Y)

        maximum = -1
        best = None
        threshold = None

        for feature in node.features:
            if len(np.unique(X[:, feature])) <= 1:
                continue
            ix = X[:, feature].argsort()
            mean_array = self.get_mean_array(np.unique(X[ix, feature]))
            for value in mean_array:  # 各中点で分割してジニ係数を計算
                lcount, lgini =\
                    self.get_gini(X[ix], Y[ix], feature, value, "left")
                rcount, rgini =\
                    self.get_gini(X[ix], Y[ix], feature, value, "right")

                count = lcount + rcount
                l_probability = lcount / count
                r_probability = rcount / count

                gain = gini - (l_probability * lgini + r_probability * rgini)
                assert gain >= 0
                if gain > maximum:  # chmax
                    best = feature
                    threshold = value
                    maximum = gain

        if best is None:
            assert len(np.unique(X[:, feature])) <= 1
        return (best, threshold)

    def fit(self):  # 決定木を生成
        self.grow(node=self.root)

    def grow(self, node):  # node以降で木を成長させる
        if node.depth >= self.max_depth:
            return

        X, Y = node.X, node.Y
        feature, threshold = self.split(node)

        if feature is None:
            return
        node.feature = feature
        node.threshold = threshold
        il, ir = X[:, feature] <= threshold, X[:, feature] > threshold
        ndepth = node.depth + 1
        node.left = Node(
            X[il],
            Y[il],
            depth=ndepth,
        )
        node.right = Node(
            X[ir],
            Y[ir],
            depth=ndepth,
        )

        self.grow(node.left)
        self.grow(node.right)

    def prune(self):  # 木の剪定 (arg{min{g(x)}}の子孫を全て削除する)
        stack = [self.root]
        N = len(self.X)
        INF = 1 << 30
        mg = (INF, None)  # min_g, arg{min_g}
        while len(stack):  # DFS
            current = stack.pop()
            has_left = current.left is not None
            has_right = current.right is not None
            is_terminal = not has_left and not has_right

            if not is_terminal:  # 非終端ノードはg(node)を計算
                expr = self.g(current)
                if expr < mg[0] and current != self.root:
                    mg = (expr, current)

            if has_left:
                stack.append(current.left)
            if has_right:
                stack.append(current.right)

        alpha, target = mg
        if target is not None:
            target.left = None
            target.right = None

        return alpha

    def get_terminal_error(self, node):  # 終端nodeの誤り率 = M(t) / N , M(t):=総誤り数
        N = len(self.X)
        failure = 0
        for y in node.Y:
            failure += y != node.class_label

        return failure / N

    def get_nonterminal_error(self, node):  # 非終端nodeの誤り率 = 再代入誤り率 * 周辺確率
        p_t = len(node.X) / len(self.X)  # 周辺確率
        R_t = node.get_error() * p_t
        return R_t

    def g(self, node):  # g(t) = node_tのリンクの強さ
        R_t = self.get_nonterminal_error(node)
        stack = [node]
        terminals = 0
        R_T = 0
        while len(stack):  # DFS
            current = stack.pop()
            has_left = current.left is not None
            has_right = current.right is not None
            if has_left:
                stack.append(current.left)
            if has_right:
                stack.append(current.right)
            if not has_left and not has_right:
                R_T += self.get_terminal_error(current)
                terminals += 1

        alpha = R_t - R_T
        alpha /= (terminals - 1)
        return alpha

    def draw(self):  # 分割区間をグラフに表示
        if not PLOT:
            return
        stack = [self.root]
        terminals = []
        while len(stack):  # DFS
            current = stack.pop()
            if current.left is not None:
                stack.append(current.left)
            if current.right is not None:
                stack.append(current.right)

            if current.feature is None:
                continue

            if not current.feature:
                plt.plot([current.threshold, current.threshold],
                         self.min_max_table[~current.feature], color="green")
            else:
                plt.plot(self.min_max_table[~current.feature], [current.threshold,
                                  current.threshold], color="green")

    def predict(self, X):  # 識別器
        predictions = np.zeros_like(X[:,0])
        for i,x in enumerate(X):
            values = {}
            for feature in self.root.features:
                values.update({feature: x[feature]})

            current = self.root
            while current.depth < self.max_depth and current.feature is not None:
                next = current.left if values[current.feature] < current.threshold else current.right
                if next is not None:
                    current = next
                else:
                    break
            predictions[i] = current.class_label

        return predictions

では, 試しに10回ほど剪定を行うようにmain関数をいじってみましょう.

def main():
    from sklearn.datasets import load_iris

    # Data-set
    iris = load_iris()
    X, Y = iris.data[:, :2], iris.target

    # Train
    tree = Tree(np.array(X), np.array(Y), max_depth=100)
    tree.fit()

    # Pruning
    for _ in range(10):
        g = tree.prune()
    
    #Test
    error = test(X, Y, tree)

    # Plot & Draw (おまじない)
    mesh = 200
    mx, my = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, mesh), np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, mesh))
    mX = np.stack([mx.ravel(),my.ravel()],1)
    mz = tree.predict(mX).reshape(mesh,mesh)

    plt.scatter(X[:, 0], X[:, 1], c=Y)
    plt.contourf(mx, my, mz, alpha=0.4, cmap='plasma', zorder=0)
    plt.savefig("result.png")

    tree.draw()
    plt.savefig("result_with_lines.png")

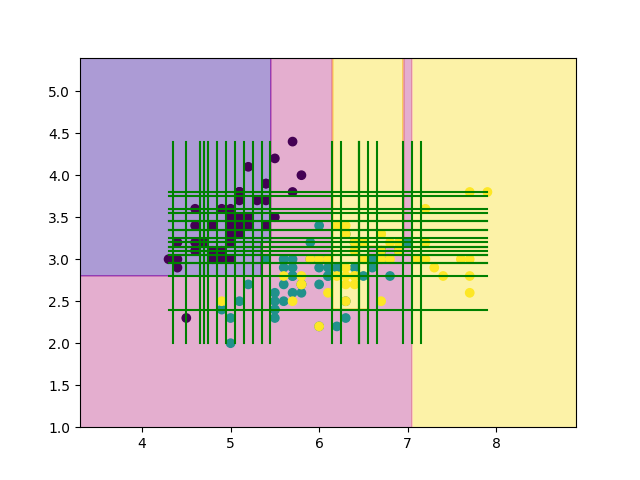
f:id:yuwd:20211218165901p:plain:w300 — 剪定回数10回としたときの実行結果

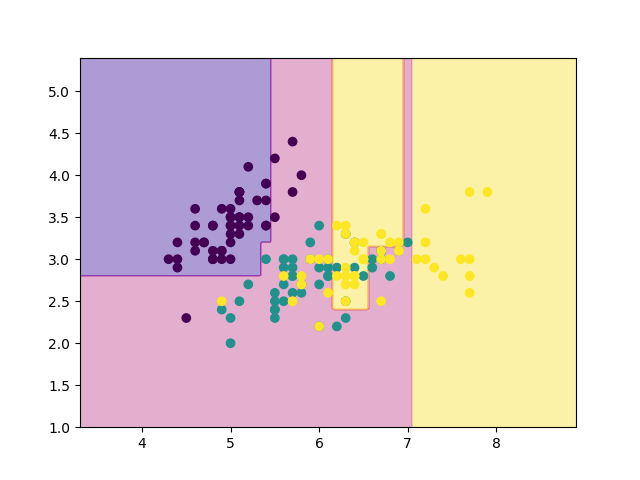
f:id:yuwd:20211218165904p:plain:w300 — 剪定回数10回としたときの実行結果

先程の結果と見比べてみると, 確かに領域が少しだけ荒くなっていますね. 再代入誤り率は19%でした.

ところで, 剪定回数はどのように決めれば良いでしょうか. はじパタによると, ホールドアウト法や交差検証法を行って決めるのが良いみたいです.

今回は交差検証を実際にやってみましょう. まずはデータを巡回しながら分割していく関数を書きます. こういうのは, ベクトル(行列)をconcatenateしてあげるとmod取らずに済むので便利です. (競プロの名残でやってるだけで, bestな方法かはよくわからないです)

def split_data(X, Y, size):  # データを分割
    window = len(Y) // size
    train_size, test_size = len(Y) - window, window
    res = []
    _X, _Y = np.concatenate((X, X)), np.concatenate((Y, Y))
    for i in range(size):
        offset = window * i
        test_tail = offset + window
        X_test, Y_test =\
            _X[offset:test_tail], _Y[offset:test_tail]
        X_train, Y_train =\
            _X[test_tail:test_tail + train_size], _Y[test_tail:test_tail+train_size]
        res.append((X_train, Y_train, X_test, Y_test))

    return res

ついでに, モデルをテストするヤツも書きましょう.

def test(X_test, Y_test, tree, log=False):  # モデルをテスト
    Xsubset = X_test
    res = tree.predict(Xsubset)
    allcount = len(Xsubset)
    correct = np.sum(res == Y_test)
    error = 1 - correct / allcount
    if log:
        print("all:", len(Xsubset))
        print("correct:", correct)

    return error

あとは, 交差検証して適切な剪定回数を探索してあげるだけです. 今回は, グリッドサーチ(という名の全探索)を行いましょう. 大体, 0~20程度で剪定が終わってしまうことが多いです.

def main():
    from sklearn.datasets import load_iris

    # Data-set
    size = 4
    searched = []

    iris = load_iris()
    X, Y = iris.data[:, :2], iris.target
    splited = split_data(X, Y, size)

    # Search-HyperParam
    models = {}
    for pruning_count in [i for i in range(20)]:
        models[pruning_count] = []
        # Train & Test
        errors = 0
        for i in range(size):
            X_train, Y_train, X_test, Y_test = splited[i]

            # Decision-tree
            tree = Tree(np.array(X_train), np.array(Y_train), max_depth=100)
            tree.fit()

            # Pruning!!
            for _ in range(pruning_count):
                g = tree.prune()

            error = test(X_test, Y_test, tree)
            models[pruning_count].append((error, tree))
            errors += error
            tree.draw()
            plt.scatter(X[:, 0], X[:, 1], c=Y)
            plt.savefig("images/figure{}.png".format(pruning_count))
            plt.clf()

        errors /= size
        print("{:.2f}, {}".format(errors, pruning_count))
        searched.append((errors, pruning_count))

    # Select-HyperParam
    searched.sort(key=lambda x: x[0])
    error, pruning_count = searched[0]
    print("pruning_count:", pruning_count)

    # Select-model
    models[pruning_count].sort(key=lambda x: x[0])
    error, tree = models[pruning_count][0]

    # Plot & Draw
    mesh = 200
    mx, my = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, mesh), np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, mesh))
    mX = np.stack([mx.ravel(), my.ravel()], 1)
    mz = tree.predict(mX).reshape(mesh, mesh)

    plt.scatter(X[:, 0], X[:, 1], c=Y)
    plt.contourf(mx, my, mz, alpha=0.4, cmap='plasma', zorder=0)
    plt.savefig("result.png")

    tree.draw()
    plt.savefig("result_with_lines.png")

    r = test(X,Y,tree)
    print("error:", round(error, 3))
    print("r:", round(r, 3))



if __name__ == "__main__":
    start = time.time()
    main()
    elapsed_time = time.time() - start
    print("time:{:.2f}[sec]".format(elapsed_time))

実行結果は以下のとおりです.

0.44, 0
0.43, 1
0.39, 2
0.41, 3
0.41, 4
0.41, 5
0.41, 6
0.41, 7
0.41, 8
0.41, 9
0.41, 10
0.41, 11
0.43, 12
0.49, 13
0.61, 14
0.61, 15
0.62, 16
0.66, 17
0.66, 18
0.66, 19
pruning_count: 2
error: 0.27
r: 0.153
time:19.07[sec]

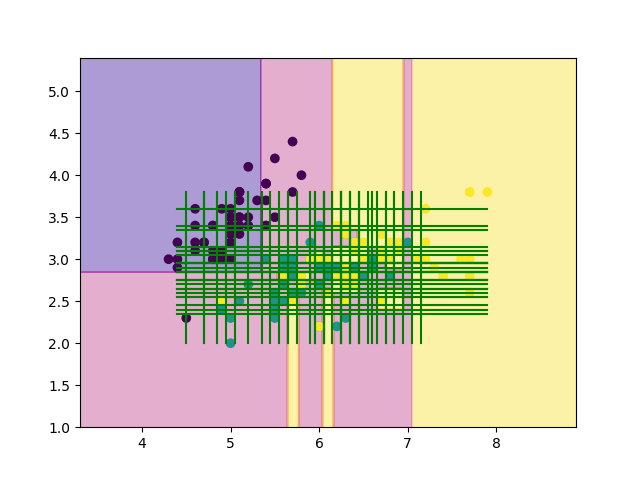
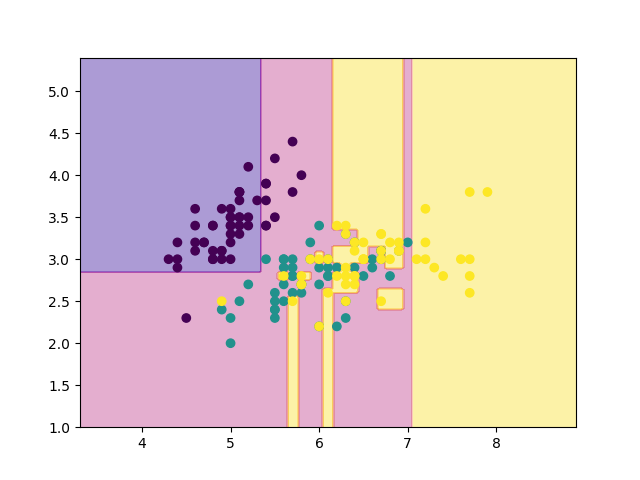
ということで, 結局今回のirisのデータセットでは, 剪定回数2回が最も良いモデルだと判断したようです. 再代入誤り率は15%でした.

iris以外のデータでも試してみよう.

同心円状に分布したデータで試してみましょう.

    X = np.random.uniform(-1,1,[500,2])
    Y = (np.sqrt(X[:,0]**2+X[:,1]**2)//0.2).astype(int)

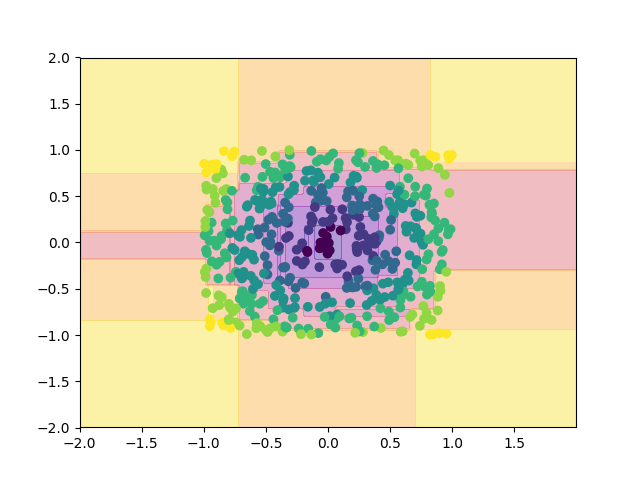
f:id:yuwd:20211218171915p:plain — 同心円状に広がったデータでの実行結果

0.24, 0
0.65, 1
0.70, 2
0.70, 3
0.70, 4
0.70, 5
0.70, 6
0.70, 7
0.70, 8
0.70, 9
0.70, 10
0.70, 11
0.70, 12
0.70, 13
0.70, 14
0.70, 15
0.70, 16
0.70, 17
0.70, 18
0.70, 19
pruning_count: 0
error: 0.216
r: 0.054
time:52.92[sec]

あれれ. 剪定0回のモデルが採用されてしまいました.

かなり複雑な木が生成されているはずですから, 剪定回数0回では汎化性能が良いとは言えなそうです.

また上の実行結果を見てみると, 剪定回数 $k = 2$ 以降の精度がほとんど変化していません. つまり, このような, 決定木では特徴を捉えにくいデータセットだと, 一度に大量のエッジを剪定してしまうというリスクがあることがこれらから読み取ことができます.

したがって実際はこのような手法ではなく, 先程登場した正則化パラメータ $\alpha$ であったり, 木の深さ max_depth を調整して学習させるのがbetterな戦略のようです.

(時間の都合上書けませんでしたが, ランダムフォレストと呼ばれる手法を使うとより良い結果が得られます. 次回, 時間があればランダムフォレストについても記事を書いてみようと思います.)

おわりに

どうでしたか？これで決定木をソラで書けるようになりましたよね？？？？？？？？

決定木には, 深層学習とは異なる面白みがあります. あまり研究のネタにはならないようですが(失礼), KaggleのようなコンペではGBDTやLightGBMなど, 決定木ベースのモデルが使われることが多々あります.

ということで, 決定木もちょっとは勉強してみて損は無いかなと思います.

久しぶりに記事を書いてみたのですが, やはり書物は面白いです.

このアドカレを機に, ちょっとずつアウトプットの頻度を増やしていけたらいいなと思ってます. アドカレを主催した@yapatta_progさんありがとうございました.

コードはgistにあげておいたので, 自由にお使いください. ここおかしいよ〜ってなったら是非コメントかTwitterで投げてみてください！

gist.github.com